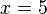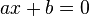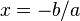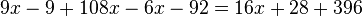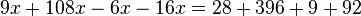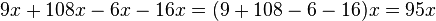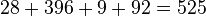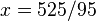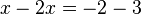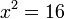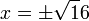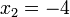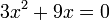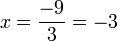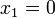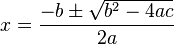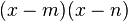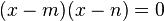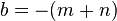¿Que son los polinomios?
Polinomio, en matemáticas, se denomina a la suma de varios monomios, llamados términos del polinomio. Es una expresión algebraica constituida por una o más variables, utilizando solamente operaciones de adición, sustracción, multiplicación y exponentes numéricos positivos. El polinomio de un sólo término se denomina monomio, el de dos binomio, el de tres trinomio.
La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:
por ejemplo:
Se denomina grado de un polinomio a la mayor potencia de los monomios que lo componen.
¿la historia de los polinomios?
La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática. Sin embargo, la elegante y práctica notación que utilizamos actualmente se desarrolló a partir del siglo XV.En el problema 14º del papiro de Moscú (ca. 1890 a. C.) se pide calcular el volumen de un tronco de pirámide cuadrangular. El escriba expone los pasos: eleva al cuadrado 2 y 4, multiplica 2 por 4, suma los anteriores resultados y multiplícalo por un tercio de 6 (h); finaliza diciendo: «ves, es 56, lo has calculado correctamente». En notación algebraica actual sería: V = h (t² + b² + tb) / 3, un polinomio de cuatro variables (V, h, t, b) que, conociendo tres, permite obtener la cuarta variable.
Algunos polinomios, como f(x) = x² + 1, no tienen ninguna raíz que sea número real. Sin embargo, si el conjunto de las raíces posibles se extiende a los números complejos, todo polinomio (no constante) tiene una raíz: ese es el enunciado del teorema fundamental del álgebra.
Hay una diferencia entre la aproximación de raíces y el descubrimiento de fórmulas concretas para ellas. Se conocen fórmulas de polinomios de hasta cuarto grado desde el siglo XVI (ver ecuación cuadrática, Gerolamo Cardano, Niccolo Fontana Tartaglia). Pero, las fórmulas para polinomios de quinto grado fueron irresolubles para los investigadores durante mucho tiempo. En 1824, Niels Henrik Abel demostró que no puede haber fórmulas generales para los polinomios de quinto grado o mayores (ver el teorema de Abel-Ruffini). Este resultado marcó el comienzo de la teoría de Galois que se ocupa del estudio detallado de las relaciones existentes entre las raíces de los polinomios.
La máquina diferencial de Charles Babbage fue diseñada para crear automáticamente tablas de valores de funciones logarítmicas y diferenciales, evaluando aproximaciones polinómicas en muchos puntos, usando el método de las diferencias de Newton.
Las funciones polinómicas son aquellas que surgen de evaluar los polinomios sobre las variables en las que están definidos. Son una clase de funciones suaves, esto es, son infinitamente diferenciables (tienen derivadas de todos los órdenes finitos).
A las funciones polinómicas de:
- Función polinómica de grado 0, que también se denomina: funciones constantes
- Función polinómica de grado 1, que también se denomina: funciones lineales,
- Función polinómica de grado 2, que también se denomina: funciones cuadráticas,
- Función polinómica de grado 3, que también se denomina: funciones cúbicas.
- Función polinómica de grado 4, que también se denomina: funciones de grado 4.
Debido a su estructura simple, los polinomios son muy sencillos de evaluar, y se usan ampliamente en análisis numérico para interpolación polinómica o para integrar numéricamente funciones más complejas. Una manera muy eficiente para evaluar polinomios es la utilización de la regla de Horner.
En álgebra lineal el polinomio característico de una matriz cuadrada codifica muchas propiedades importantes de la matriz. En teoría de los grafos el polinomio cromático de un grafo codifica las distintas maneras de colorear los vértices del grafo usando x colores.
Con el desarrollo de la computadora, los polinomios han sido remplazados por funciones spline en muchas áreas del análisis numérico. Las splines se definen a partir de polinomios y tienen mayor flexibilidad que los polinomios ordinarios cuando definen funciones simples y suaves. Éstas son usadas en la interpolación spline y en gráficos por computadora.
operaciones de polinomios:
Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes. Para multiplicar polinomios se multiplica cada término de un monomio por el término del otro monomio y se simplifican los monomios semejantes, posteriormente.Factorización [editar]
Para factorizar un polinomio de segundo grado completo (con todos los términos) se divide por el inverso de una de sus raíces sumado con la incógnita, siendo los factores el número por el que dividimos y el resultado; ya que no hay resto, cumpliéndose así que dividendo = divisor Χ cociente + resto. En caso de que el polinomio no tenga término independiente se sacará la incógnita como factor común y ya está factorizado. También se puede factorizar usando las igualdades notables.
Ejemplos [editar]
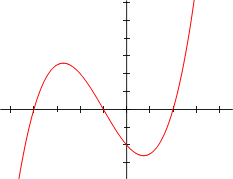
Las funciones polinómicas de una variable (x), se corresponden con diversas curvas planas, que se pueden representar en un sistema de coordenadas cartesianas XY.
La función
es un ejemplo de función polinómica con coeficiente principal 13 y una constante de 3.
Un polinomio es una expresión con letras y números sumados y multiplicados
P(x,y)=x y 2+2x-3y+5y3-1 los numeros se denominan coeficientes y las letras variables
La maxima potencia de las variables se llama grado del polinomio .
Estudiaremos polinomios con una sola variable ej: p(x)=x3-3x2+5x-1 es un polinomio de tercer grado La Suma
Operación suma: la suma de dos polinomios se hace sacando factor común a la misma potencia de la variable. (x3-3x2+5x-1)+( 2x3+x2-2x+1)= (1+2)x3+(-3+1)x2+(5-2)x-(1-1)
La resta de la misma manera pero restando los numeros.
La multiplicación :
la multiplicación se realiza haciendo uso de la propiedad distributiva esto es multiplicando (signos variables y coeficientes) cada uno del primer factor por todos los del segundo .

La división :
Para realizar la division ajustaremos(signos variables y coeficientes de los primeros sumandos del dividendo y del divisor , multiplicamos este or el divisor y los restamos del dividendo bajando la siguiente suma asi hasta que el grado del resto es menor que el grado del divisor.
 Se cumple la prueba de la división D(x)=d(x)·c(x)+r(x)
Se cumple la prueba de la división D(x)=d(x)·c(x)+r(x)
3x3-4x2+2x-1=(x-3)·(3x2+5x+17) +50
valor
Valor : se llama valor de un polinomio P(x) en un punto x=a al resultado de substituir la x por a P(a)
Ej : x3-3x2+5x-1 en x=2 es 23-3·22+5·2-1
ceros
Se llama cero de un polinomio a una substitucion de la x tal que su valor sea cero esto es P(a)=0
Ej: x2-9 en x=3 vale cero luego decimos que 3 es un cero de x2-9
Si nos fijamos en la división del ejemplo el numero 3 es un cero del polinomio divisor (x-3)
Si substituimos la prueba 3x3-4x2+2x-1=(x-3)·(3x2+5x+17) +50 la x® 3 queda
prueba 3 33-4 32+2 3-1=(3-3)·(3 32+5 3+17) +50=50 pues 3-3=0
TEOREMA DEL RESTO:
EL Resto de la division de dos polinomios puede calcularse: haciendo la división o substituyendo en el dividendo los ceros del divisor
Pues bien al igual que con los números un polinomio es divisible por otro cuando al hacer la division el resto sea cero . y un polinomio primo a aquel que no tiene divisores.
POLINOMIOS PRIMOS
Polinomios primos serán los de primer grado esto es de la forma (x ± a) pues si no fuesen primos habría otros que lo dividiría y tendría un grado menor pero esto no puede ser.
DIVISIBILIDAD
Teorema : Los divisores de un polinomio serán pues de la forma (x- sus ceros) , cuando los tengan de lo contrarios tambien serían primos.
Si P(x) es divisible por (x-a) el resto será cero pero por el teorema del resto este resto es el valor de P(a)
Por tanto a será tal que P(a)=0 o sea un cero de P(x).
Teorema de factorización
 Un polinomio factoriza como producto de el coeficiente de maximo grado por el producto de (x- ceros)
Un polinomio factoriza como producto de el coeficiente de maximo grado por el producto de (x- ceros)

Sumas de Cardano:

Si de lo visto obtenemos una regla general sera la que sigue:
Termino independiente sera la multiplicación de todos los n ceros ± segun que sea par o impar la cantidad
El termino en x sera la suma de todas las n-1 multiplicaciones que se puedan hacer con los ceros cambiando el signo del anterior
El coeficiente de x2 sera la suma de todas las n-2 multiplicaciones posibles cambiando el signo del anterior
Y así el coeficiente de xk será la suma de todas las n-k multiplicaciones posibles que se puedan hacer con los ceros.
Ejemplo :
Encontrar un polinomio que tenga por ceros : 1, 2, 3
X3-(1+2+3)x2+(1·2+1·3+2·3)x-(1·2·3)=x3-6x2+11x-6
Lo que se ve inmediatamnete es que los ceros de un polinomio tienen que ser divisores del termino independiente.
De esta conclusión Ruffini se valió para encontrar un mecanismo de ensayo y error para encontrar los ceros enteros de un polinomio.
 El mecanismo es el que sigue en el organigrama de la figura para encontrar ceros que sean enteros:
El mecanismo es el que sigue en el organigrama de la figura para encontrar ceros que sean enteros:
Para encontrar ceros fraccionarios y siempre en el caso de que no hayan suficientes enteros
 Ej:
Ej:
12x3+16x2+7x+1=0
y aplicamos ruffini para calcular el valor de b ; si no se encuentra
en la ecuación hacemos a=2 y así consecutivamente hasta obtener los tres ceros.

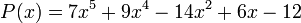



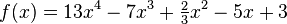

 Resuelve la ecuaciones:
Resuelve la ecuaciones: